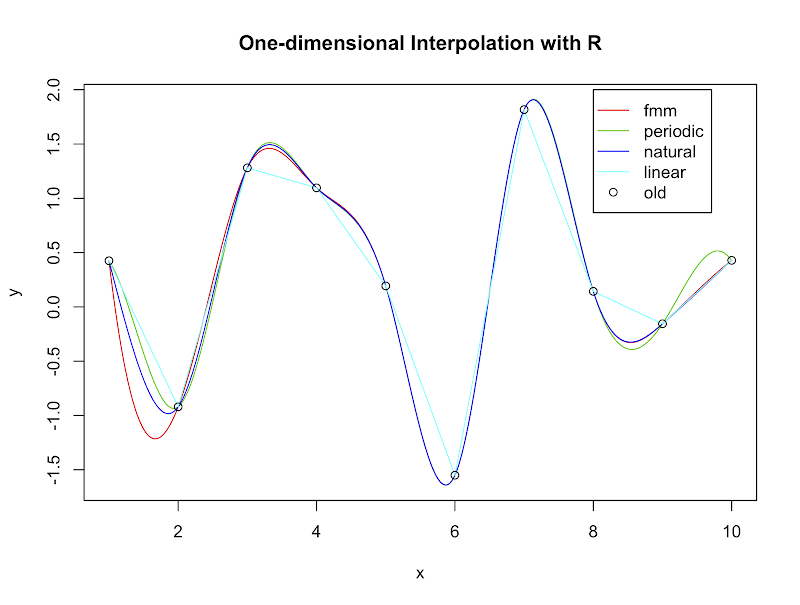
The function approx() and spline() provide one-dimensional linear and non-linear interpolation with R, respectively. Syntax of them are similar, for example,
x.old <- 1:10
y.old <- rnorm(10)
x.new <- seq(1, 10, 0.001)
# Linear interpolation
y.new.linear <- approx(x.old, y.old, xout = x.new)$y
# Forsythe, Malcolm and Moler's spline (default of spline)
y.new.fmm <- spline(x.old, y.old, xout = x.new, method = "fmm")$y
# Natural splines
y.new.natural <-
spline(x.old, y.old, xout = x.new, method = "natural")$y
# Periodic splines
y.new.periodic <-
spline(x.old, y.old, xout = x.new, method = "periodic")$y
# Plot
plot(
y.new.fmm ~ x.new,
type="l", col=2, xlab="x", ylab="y",
main="One-dimensional Interpolation with R"
)
lines(y.new.periodic ~ x.new, col=3)
lines(y.new.natural ~ x.new, col=4)
lines(y.new.linear ~ x.new, col=5)
points(y.old ~ x.old)
legend(8, 2, c("fmm", "periodic", "natural", "linear", "old"),
col = c(2:5,1), lty = c(1,1,1,1,0), pch = c(NA,NA,NA,NA,1), merge = T
)